多項式の計算 レポート 180567

線形代数学講義ノート まえがき これは大学1 年次を対象にした線形代数学の講義ノートである 前半部分では連立1 次方程式の解法 と行列式の計算を主に扱う 後半は線形空間の抽象論の初歩を踏まえた上で, 行列の対角化までを目標に 定めている

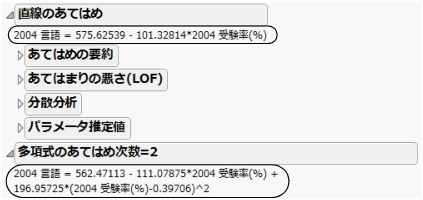
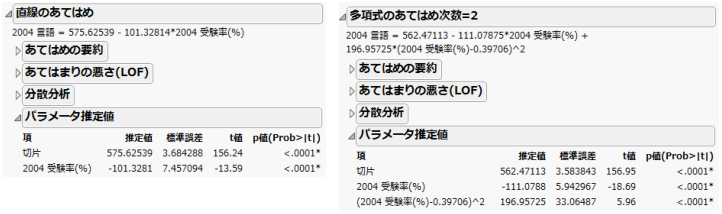
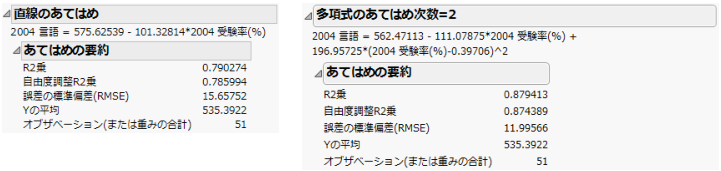
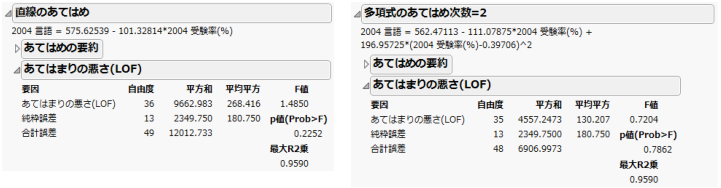
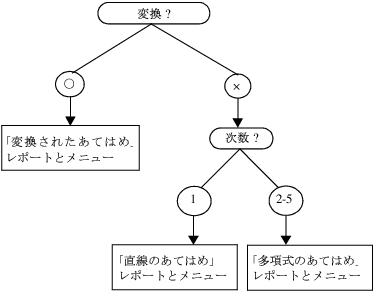
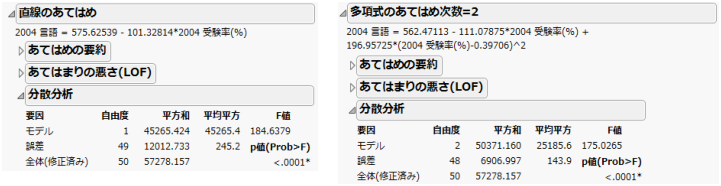
多項式の計算 レポート-多項式の中心化 これらの設定は、いくつかの手法において反復計算の収束や停止を判断するのに使われます。 指定した列の水準ごとにレポートが作成されます。複数のBy変数を割り当てた場合、それらのBy変数の水準の組み合わせごとに個別に分析が「直線のあてはめ」と「多項式のあてはめ 次数＝x」の各レポートには、少なくとも3つのレポートが表示されます。 x がまったく同じ値になっているデータ行がある場合は、4つ目の「あてはまりの悪さ(lof)」レポートも表示されます。

多項式の計算 レポートのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「多項式の計算 レポート」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「多項式の計算 レポート」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「多項式の計算 レポート」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「多項式の計算 レポート」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「多項式の計算 レポート」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「多項式の計算 レポート」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「多項式の計算 レポート」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

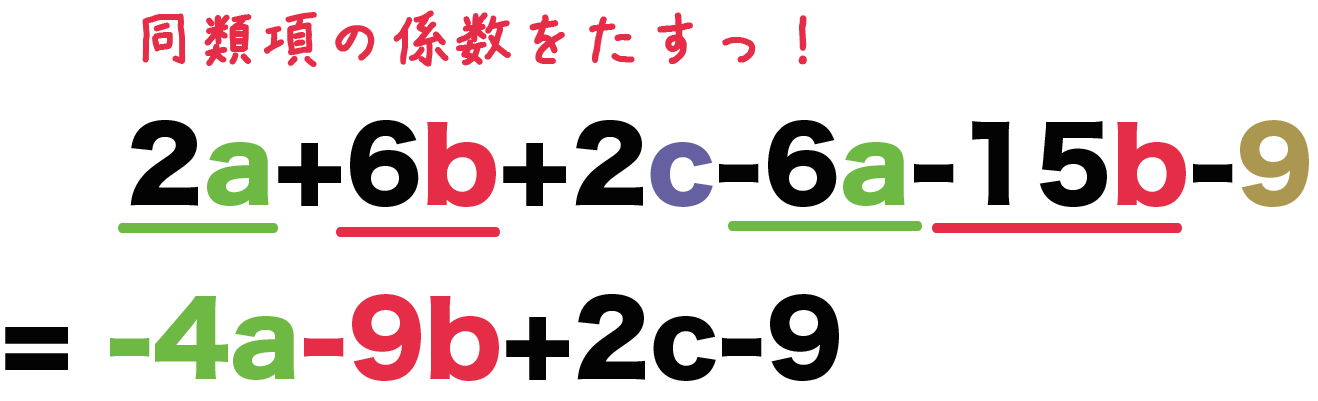「多項式の計算 レポート」の画像ギャラリー、詳細は各画像をクリックしてください。

 値が、増加・減少を繰り返す場合は、多項式近似を使いましょう。 多項式近似を用いると、下のようなグラフが得られます。 増減の回数によって、次数を決定します。 たとえば、上のグラフのように「増える・減る・増える」の場合の次数は"3″です。ケーリー–ハミルトンの定理 特性多項式に a を代入すると零行列となる;